Our main objective is to become a reference research centre in the development and innovation in Applied Mathematics. We support all kind of projects in engineering, medicine, economy…
You can see a list of research lines below.
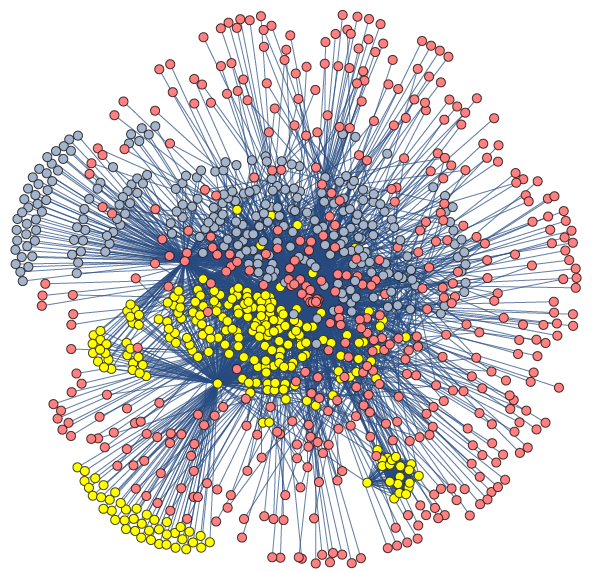
Analysis of complex networks
The research field focused on complex networks has increased in recent years due to the advance in knowledge about the interplay between the structure of a network (topological properties, centrality measures, community detection, etc.) and the function of the nodes (influential actors, developers of new ideas, intermediaries between new technologies, etc.). Moreover, the huge quantity of available data has led to new definitions of traditional concepts related to networks such as centrality measures, spreading processes, robustness, etc.
Our study is aimed to focus on the mathematical foundations of these new concepts and the ways in which these tools could be implemented. In particular, during the next three years, our objective is to study some mathematical properties of Multiplex Networks related to the features of the eigenvalues and eigenvectors of some matrices associated to the Multiplex. In particular, we focus on several definitions of Multiplex PageRank existing in the current literature with the aim of comparing their outcomes in test cases, their mathematical properties (such as velocity of convergence), and their ability to bias the ranking to some nodes.
Application of bioinspired optimization algorithms
This research area arose inside the research area “Modeling the transmission dynamics of infectious diseases” where we used bioinspired optimization algorithms to find the parameters of the model that best describe a given (observed) infectious.
Taking into account the inherent uncertainty in the evolution of infectious diseases described on networks, bioinspired optimization algorithms are proving to be a very effective tool to set their dynamics description of transmission. Apart from the application described above about fitting models to data, this type of algorithms is applicable to all kinds of complex problems of optimization in engineering and other science
Design of improved concretes / mortars from the addition of industrial, agronomic and construction waste
The waste coming from different sectors improves the mechanical characteristics of the concrete, modifies the susceptibility of it to external aggressions (for example, chlorides …) and extends its useful life. It is a component of great value for all those companies that wish to add value to their waste or obtain improved concrete at a competitive price.
In this field, researchers from the Multidisciplinary Mathematics Institute of the Universidad Politecnica de Valencia work with two very common waste: slag and recycled rubber from Tires Out of Use (NFU). These residues provide concrete / mortar with special characteristics that make them especially useful for very specific uses.
The high density of copper slag makes it to be added to concrete, in specific dosages and granulometry, it acquires a high density. By means of this technique, high performance concretes are being obtained that are used for very specific uses. As an example, the group has extensive experience in the use of these concretes in port docks and in the manufacture of an artificial ballast to minimize the phenomenon of ballast flight.
On the other hand, the elastic characteristics of recycled rubber, coming from the NFU, allows to create compressible mortars with very specific applications and valued in the processes of excavation of tunnels through the use of tunnel boring machines.
The researchers have developed projects in which slag has already been introduced and high-density concrete has been obtained for railway and port uses. This line of work is being perfected based on the analysis of new waste.
Design, analysis and stability of iterative processes for solving nonlinear equations, systems and nonlinear matrix equations (DAMRES).
 The design, analysis and implementation of iterative methods for solving nonlinear models is a broad area of research that is extremely important in the field of Numerical Analysis and, in general, for any applied science. A large number of problems in Science and Engineering require the solution of this type of equations.
Our lines of research can be summarized as follows
The design, analysis and implementation of iterative methods for solving nonlinear models is a broad area of research that is extremely important in the field of Numerical Analysis and, in general, for any applied science. A large number of problems in Science and Engineering require the solution of this type of equations.
Our lines of research can be summarized as follows
- Multipoint iterative methods, with and without memory.
- Steffensen type iterative schemes.
- Iterative procedures for singular problems: multiple roots, singular Jacobian matrices, ill-conditioned matrices.
- Interval methods for solving nonlinear equations and systems.
- Nonlinear matrix equations with iterative methods.
- Design and analysis of algorithms for obtaining inverses and pseudoinverses.
- Dynamic behavior of the rational operator associated to any iterative process.
- Numerical solution of PDEs (wave equation, Burger equation, Fisher equation...).
- Algorithms for the preliminary determination of the orbit of artificial satellites.
- Dynamic models of chemical reactors.
- Electromagnetic problems.
- Digital image processing.
Members:
- Juan R. Torregrosa (Universitat Politècnica de València)
- Alicia Cordero (Universitat Politècnica de València)
- Eulalia Martínez (Universitat Politècnica de València)
- Neus Garrido (Universidad Internacional de la Rioja)
- Cristina Jordán (Universitat Politècnica de València)
- Esther Sanabria (Universitat Politècnica de València)
- Francisco Chicharro (Universitat Politècnica de València)
- Rafael R. Capdevila (Universitat Politècnica de València)
- Pura Vindel (Universitat Jaume I)
- Beatriz Campos (Universitat Jaume I)
- María P. Vassileva (Instituto Tecnológico de Santo Domingo)
- Santiago Artidiello (Instituto Tecnológico de Santo Domingo)
- Javier G. Maimó (Instituto Tecnológico de Santo Domingo)
Development of nuclear reactor simulators
 For design and safety reasons, nuclear power plants need fast and accurate plant simulators. Nuclear power plants basically consist of a steam generator system, called the nuclear steam supply system and a turbo generator which converts the steam energy into electricity. The energy used to produce steam comes from basic nuclear reactions induced by neutrons in the nuclear fuel of the reactor core. Plant simulators mainly consist of two different modules which acount for the basic physical phenomena taking place in the plant. A neutronic module which simulates the neutron balance in the reactor core, and a thermalhydraulic module which simulates the heat transfer from the fuel to the coolant, and the evaporation and condensation processes.
We focus on the neutronic module. The balance of neutrons in the core is given by neutron transport equation, but to solve this equation is a very difficult problem. Thus, different approximations are considered as the neutron diffusion equation or higher order approximations as the SPN and the PN equations. In this line of research, different approaches have been used to solve these equations to study the steady state of the reactor core and also to study different transients. These problems are very big for a commercial reactor and efficient codes, based on advanced algebraic methods, have been developed to solve these equations.
Detailed information on the research can be found on the FEMFFUSION website..
For design and safety reasons, nuclear power plants need fast and accurate plant simulators. Nuclear power plants basically consist of a steam generator system, called the nuclear steam supply system and a turbo generator which converts the steam energy into electricity. The energy used to produce steam comes from basic nuclear reactions induced by neutrons in the nuclear fuel of the reactor core. Plant simulators mainly consist of two different modules which acount for the basic physical phenomena taking place in the plant. A neutronic module which simulates the neutron balance in the reactor core, and a thermalhydraulic module which simulates the heat transfer from the fuel to the coolant, and the evaporation and condensation processes.
We focus on the neutronic module. The balance of neutrons in the core is given by neutron transport equation, but to solve this equation is a very difficult problem. Thus, different approximations are considered as the neutron diffusion equation or higher order approximations as the SPN and the PN equations. In this line of research, different approaches have been used to solve these equations to study the steady state of the reactor core and also to study different transients. These problems are very big for a commercial reactor and efficient codes, based on advanced algebraic methods, have been developed to solve these equations.
Detailed information on the research can be found on the FEMFFUSION website..
Dynamical systems with uncertainty and applications
Deterministic mathematical models based upon difference, differential, integro-differential equations are, to certain point of view, very useful to represent the complex reality in different scientific and technical fields. The formulation of such models requires, in practice, exhaustive measurements of relevant variables in order to evaluate the different parameters of the model. This implies a level of uncertainty, as a consequence of measurements errors, and randomness must be introduced in the formulation of these models from the very beginning.
For example: the propagation of a biological species depends on its growth rate, which is influenced by a large number of environmental and genetic factors whose complex behaviour cannot be considered deterministic; geological phenomena such as earthquake displacements requires the introduction of spatial randomness into the model in order to describe properly the grounds heterogeneities, the determination of prices of financial options is a function of the sophisticated conditions on global markets depending on random factors such as the investment confidence, international political risks or the decisions imposed by governments.
This random approach, closer to the complexity of reality instead of classical deterministic approaches, makes more reasonable to include randomness into the formulation of mathematical models based upon difference, differential, integro-differential equations which can be useful to scientific applications.
The main research lines of the group are:
- Analytical and numerical techniques to approximate the solution of random ordinary, partial and differential equations as well as their main statistical moments (mean, variance, etc.).
- Determination of the probability density function of the solution of these kind of random systems.
- Parameter estimation and Uncertainty Quantification of models based on random systems (Epidemiology, Finance, Medicine, etc.).
General systems theory
General Systems Theory seeks a universal language for all scientific disciplines. Less ambitious too, but also important and more practical is the aim of looking for general systems. General systems are mathematical models, products of the abstraction of particular systems in more abstract models that encompass the individual ones. The fruit of this objective is the extension of the quantum formulation from the physical systems to the general dynamical systems.
On the other hand, another objective of the line of research considers that the starting point is the generalization that Antonio Caselles realized of the System Dynamics invented by Jay W. Forrester in the MIT. This generalization introduced a mathematical formulation of System Dynamics and the possibility of working with deterministic or stochastic systems. The topic addressed from this perspective is known as “Country Development”, that is, the study of the development of a country or society. With the models obtained we can study crucial issues for human societies such as sustainability and population replacement, unemployment, environmental impact or happiness.
Finally, another objective starts from the Unique Trait Personality Theory of Salvador Amigó, which in the current literature is known as General Factor of Personality (GFP). This theory proposes to GFP as a single factor that can explain the global personality of an individual, and that it encompasses the theory of the three factors of Eysenck and that of the Big Five. Currently our research focuses on the reproduction of the effects of a drug without using the drug through Salvador Amigó‘s Self-Regulation Therapy and its simulation with dynamical stimulus-response models.
Geometric numerical integration
Differential equations constitute one of the most important tools for modeling the evolution in time of natural phenomena: planetary motion, particle accelerators, fluid mechanics, population dynamics, molecular dynamics, etc. The theory of differential equations comprises many different mathematical fields, and the problems arising in that theory have made fundamental contributions to linear algebra, the theory of Lie groups, and functional analysis. There are types of problems arising in many fields of science and applied mathematics that possess an underlying geometric structure which influences the qualitative character of their solutions and so one aims naturally to construct numerical approximations that preserve this geometry. However, many numerical integrators included in standard software packages do no take into account these distinctive features of the equations to be solved.
The goal is to design new schemes providing approximate solutions that share one or several geometries properties with the exact solution to have a numerical method with an improved qualitative behavior, but also provide more accurate long-time integration results than those obtained by general-purpose algorithms. This is precisely the realm of Geometric Numerical Integration. Our research group mainly focuses in the analysis and development of new geometric integrators that can be used to the study of problems in Celestial Mechanics (e.g. to study the evolution of the Solar System or trajectories of satellites), Quantum Mechanics, Monte Carlo, optimal control, etc.
The main research areas are:
- Splitting methods (when the system is separable in solvable parts or easier to deal with).
- Methods based on the Magnus series.
High performance scientific computing (Group HiPerSC)
 This group is made up of a total of 6 researchers, of which two belong to the Institute of Multidisciplinary Mathematics, and the rest are researchers from the Institute of Instrumentation for Molecular Imaging, of the Institute of Telecommunications and Multimedia Applications, and of the Department of Computer Systems and Computing. The group is multidisciplinary and focuses on applied mathematics and its applications, in particular the development of efficient methodsfor scientific computation in the area of differential equations, the functions of matrices, and their applications. Moreover, it specializes on the development of high-performance computing and its scientific applications.
Detailed information about the ongoing work, articles, developed software can be found on the web page of the group.
This group is made up of a total of 6 researchers, of which two belong to the Institute of Multidisciplinary Mathematics, and the rest are researchers from the Institute of Instrumentation for Molecular Imaging, of the Institute of Telecommunications and Multimedia Applications, and of the Department of Computer Systems and Computing. The group is multidisciplinary and focuses on applied mathematics and its applications, in particular the development of efficient methodsfor scientific computation in the area of differential equations, the functions of matrices, and their applications. Moreover, it specializes on the development of high-performance computing and its scientific applications.
Detailed information about the ongoing work, articles, developed software can be found on the web page of the group.
Inspection and analysis of structures based on an algorithm for ultrasonic methods that allows the treatment of the image obtained
The control and assurance of quality in structures has become a fundamental activity in the industry, whether in structural conditions, equipment, parts or assemblies, to ensure the reliability of the assets and the continuity of the operation. A defect in these can cause premature failure and, therefore, entail significant economic, social and environmental risks. From this necessity arose the Non Destructive Tests, END, main technique for the execution of activities of quality control in structures. Among the different technologies to carry out the analyzes, ultrasounds are one of the most used methods due to their low cost and their ability to detect internal defects. However, this technology has technical-economic limitations that lead to a loss of accuracy and errors in the diagnosis of failures as well as high implementation costs.
In this sense, the research group of the Multidisciplinary Mathematics Institute of the UPV, coordinated by Professor Julia Real, has extensive experience in systems of prediction and maintenance of structures.
Regarding the analysis of defects in structures by ultrasound, this group develops an algorithm of pre-processing of ultrasonic signals based on the implementation of multi-scale noise elimination methods (multiresolution), through the Wavelet Packet Transformation, for the decomposition of the image in sub-images easier to process and the subsequent application of a self-adaptive threshold for speckle noise cancellation that occurs in each of the obtained ultrasonic sub-images. Finally, a processing system capable of recognizing the type of damage presented by the structure is designed by means of the development of algorithms for the extraction of characteristics and classification of defects based on artificial neural networks. The advantage of the work developed by the IMM researchers in the inspection and analysis of structures based on algorithms for ultrasonic methods, and their subsequent defect classification algorithm, is that thanks to the elimination of multi-scale noise and speckle noise reduction , the resulting ultrasonic images are more powerful in terms of extracting conclusions. It gives the defect classification system reliable information with a low cost process, without forgetting the benefits in terms of security and damage control that a system that allows analyzing the quality of a structure entails.
In summary, through the treatment of ultrasonic signals, the research group of the Multidisciplinary Mathematics Institute develops systems for the detection and analysis, economic and of high technical capacities, of defects in structures.
Low cost monitoring of civil infrastructure and industrial systems
The great economic growth of the last times has propitiated the construction of more and better infrastructures that cover the needs of the society. However, in an economic context like the current one, it is essential to stop this continuous growth and change the mentality from an “expand” to a clear “maintain”.
Unfortunately, the existing techniques still require heavy investments. For this reason, researchers from the Multidisciplinary Mathematics Institute of the Universitat Politècnica de València are working on the development and application of new low-cost engineering monitoring systems that, taking advantage of existing technologies, represent an advance over current technology without giving up the quality of the results. In this way a competitive advantage is obtained with respect to the current solutions that facilitates the orientation of the new product towards the market by means of the implementation of a customized solution to each need.
Through the integration of low cost sensors (hardware), mathematical algorithms (software) and wireless transmission (communications system), these systems allow to know continuously and in real time the state of conservation of civil infrastructures (such as railways, tunnels or roads) and industrial systems (such as wind farms, water distribution networks or conveyor belts). All this without resorting to complex wired installations that, in numerous occasions, can make their implementation unfeasible.
The research group of the Multidisciplinary Mathematics Institute of the UPV, led by Professor Julia Real, has extensive experience in this field, which has led to registered patents of great utility for the productive sector. The group is made up of a multidisciplinary team of engineers of various kinds (industrial, civil, or telecommunications among others).
Mathematical modelling of fluid systems (Group FluIng-IMM)
In the water industry the following capabilities are essential:
- Possibility of evaluating the problems associated with the various essential elements in the management of water supply facilities.
- Have safer strategies, roadmaps and processes that allow an improved management of water supply systems.
- To specify elements of improvement in the use of resources, mitigation of technological risks, reduction of the expenses, improvement of the performance, and consolidation of the functionality of applications in the field of the water.
Matrix analysis and application to control systems
This group is integrated by 12 researchers and we are interested on the study properties related to different Matrix Analysis settings and their Applications. Some of them correspond to applications to the mathematical theory of control systems for modelling real processes (biological, economic, biomedical and agronomic).
In this study, it is necessary to know more on the underlying Matrix Theory, which are projection matrices, generalized inverses, involutory matrices, the Jordan structure the singular value decomposition of singular matrices, and factorizations of totally positive matrices. This matrix information will be used to obtain conditions for the structured control system parameters are identifiable and to construct algorithms that determine these variables. Structured systems may be subject to disturbance, therefore the stability of parameter-dependent systems where you can analyze the type of disturbances and their range of variation is considered in this project. Applying mathematical models to control problems of Agronomy is one of the objectives, as well as characterization of quasi-positive systems and their applications, in order to the theory derived above can be used in real systems. Additionally, the study of bidimensional control systems (2-D) is another objective, concretely, we will focus on the local reachability index of these systems. Since most of these subjects involve singular matrices, Generalized Inverses provide an adequate tool to work with. Approches such as optimization, nonnegative matrices, and partial orders on specific classes of matrices provide us a deeper understunding of the applications.
Our major interests are summarized as:
- Matrix Analysis in positive control systems using permutation and involutory matrices.
- Jordan form of square singular matrices, singular value decomposition of rectangular singular matrices and applications.
- Identifiability property for the structured control systems.
- Stability of parameter-dependent systems.
- Modelization of control problems in Agronomy and characterization of quasi-positive systems and their applications.
- Local reachability index of bidimensional control systems (2-D).
- Generalized inverses: theoretical and applied approaches such as optimization and partial orders.
Modelling the transmission dynamics of infectious diseases
 Mathematical epidemiology is a multidisciplinary area where medicine and mathematics can work together in order to understand the mechanisms behind the viruses and bacteria spread and transmission among individuals and/or animals.
Our team works on the model design, mainly of networks, which we adapt to existing scenarios of interest where an infectious disease is affecting a population. This way, once described the situation of interest, we can simulate the application of public health strategies, mainly vaccine programs, and study its cost and effectiveness. During the time that we have been working with the Area of Vaccines of FISABIO, we have studied C, B, and W-135 meningococci, respiratory syncytial virus, human papilloma virus, varicella, and in some of them, we have proposed public health strategies that they have been implemented.
Mathematical epidemiology is a multidisciplinary area where medicine and mathematics can work together in order to understand the mechanisms behind the viruses and bacteria spread and transmission among individuals and/or animals.
Our team works on the model design, mainly of networks, which we adapt to existing scenarios of interest where an infectious disease is affecting a population. This way, once described the situation of interest, we can simulate the application of public health strategies, mainly vaccine programs, and study its cost and effectiveness. During the time that we have been working with the Area of Vaccines of FISABIO, we have studied C, B, and W-135 meningococci, respiratory syncytial virus, human papilloma virus, varicella, and in some of them, we have proposed public health strategies that they have been implemented.
Numerical analysis and computing in finance
The modern theory of finance and especially the areas of financial derivatives and financial engineering depend strongly on mathematics. Since the subject was kick-started by the work of Black and Scholes and Merton there has been a very fruitful two-way technology transfer between a range of areas of mathematics and the financial applications. While the standard Black Scholes model was the single most important step in the development of modern derivative asset analysis, the underlying assumptions of constant volatility and a perfectly liquid market are clearly at odds with reality. As a consequence a number of approaches have been developed for dealing with the pricing and, in particular, the hedging of derivatives taking into account the issues having influences in the reality of imperfect markets. Thus, several mathematical models have been proposed in the context of limited liquidity and taking into account transaction costs. Also stochastic volatility models and jump diffusion models have been developed giving rise to linear and nonlinear partial integro-differential equations.
In practice, numerical algorithms for solution of these models are required. Our goal is to construct efficient numerical methods for financial problems, not only regarding to the computational point of view but also paying attention to the quality of the approximation throughout the careful numerical analysis of the proposed numerical schemes. Careless numerical computations may waste a good mathematical model. Several numerical techniques as finite difference schemes, semidiscretization approaches, meshfree methods, numerical integration quadrature rules, techniques to solve free boundary problems like front fixing transformations or penalty methods, are tasks to develop in this research line. The validation and the simulation of the approximating solution will be also considered in our projects.
Photocatalytic asphalt development
The levels of pollution are becoming increasingly high in big cities; this fact, together with the growing regulatory requirements regarding their control, obliges administrations to implement the necessary steps to minimize the existent pollution in their environment. Amongst the most harmful contaminants we find the sulphur oxides, mainly originated by road traffic. The researches conduced show how formulated compounds from titanium dioxide have a positive effect minimizing nitrogen oxides levels.
The Instituto Universitario Matemática Multidisciplinar of UPV has deepened into the incorporation of various compounds based on titanium dioxide in certain types of asphalt mixes (depending on its chemical composition) and has evaluated mathematically the speed at which the mix may lose its decontaminating properties. At first, its application covers asphalt mixes assigned to a wearing course in a road pack, in those environments in which pollution levels are remarkable. The use of these compounds does not disable the sound-insulating function of the asphalt mixes, therefore; both can coexist without a problem. Amongst the major advantages of the work carried out by the UPV researchers, we would like to remark the minimization of the pollution levels, mainly caused by nitrous oxides and, thus, resulting on an improvement in air quality.
Prediction and evaluation of vibrations produced by trains on railway tracks
The construction of new railway lines or the burial of old railway lines has raised the social interest for vibrations in urban areas in recent years. Especially, these vibrations affect the daily life of people who live or work near the tracks.
In this framework, the IMM research group led by Julia Irene Real Herraiz has an analytical model capable of predicting and evaluating the vibrations produced by the train when it is travelling on the road. This mathematical model allows obtaining the transmission of vibrations from the generation point (wheel-rail contact) to the surrounding terrain in both temporal and spectral terms.
The model developed by the researchers of the UPV acts as a virtual testing laboratory. In this way, it is possible to study in a fast, economic and versatile way how important parameters such as the quality of the terrain, the type of train or the speed of operation of the vehicles affect the transmission of vibrations. This aspect provides a great advantage over real-scale experiments, hence the importance of this model in the sector. As a final aim, this mathematical tool can also be used to study different methods of attenuation of vibrations, whose implementation can be addressed both in construction and exploitation.
In addition to studying these attenuation methodologies, it is also possible to know how the quality and suitability of the usual materials used in the track package for mitigating vibrations influences. Thus, this model allows us to propose improvements, make comparisons between different products of the market and propose new strategies and technologies for the future attenuation of this dynamic phenomenon so linked to rail.
This Research Unit, within the framework of the UPV, has extensive experience in the railway sector both in road design projects and in those for which it is necessary to propose a study of vibrational attenuation in the form of externality or internality to the system. To do this, this team works together with both public and private companies, which allows you to always develop useful and advantageous products for an increasingly demanding market.
Study of modelling problems and application of complex networks in social and education models
The analysis of the model of access to the University can be represented by a directed graph. A directed graph can be considered as the representation of a complex network. Especially important is the study of those elements that are closely related. It creates a group of elements in the structure that are highly connected to each other and little connected to the rest, what we call communities. This concept is related to the high density of connections in the graph. The finding of communities in a network brings us closer to the knowledge of its structure and properties. Hence the importance of the design of algorithms that allow us to obtain communities in a network, especially in the case of directed networks.
Technical management of water distribution systems (Group FluIng-IMM)
Water supply systems (WSS) are very complex structures to deal with due to the nature of the classical hydraulic models describing WSS phenomena, and due to the recent and growing need to properly handle huge amounts of data, which are generated in the various processes associated with water supply. Proper design (for new systems) and renovation (extension, rehabilitation, etc., at later stages) of water supply systems to provide the intended service are paramount; proper monitoring to obtain sufficient elements of quality judgement for (real-time) control is now crucial; optimal operation to provide a seamless quality service is vital; and finally, intelligent management capable of reconciling such conflicting objectives as economic revenue and social satisfaction is a sine qua non condition for dealing with water supply systems.
Effective mathematical techniques are needed to deal with the complexity of the problems associated with drinking water and sanitation services. For example, in design and retrofitting tasks, robust and efficient optimisation algorithms, capable of dealing with non-linearities, mixed variables and discrete processes, including those of an evolutionary nature, are paramount. Real-time monitoring of quality of service will benefit from efficient time series data processing techniques, including a number of mathematical transformations. Performance can be defined in terms of a set of optimally defined Boolean operators embedded in appropriate data structures, again relying on other types of optimisation techniques. Finally, management is currently addressed across a wide spectrum of issues including demand forecasting, network sectorisation, leakage detection, cadastre maintenance, customer satisfaction assessment, etc. Widely used soft computing techniques such as neural networks, support vector machines, clustering, agent-based systems, social network theory, etc. are expected to be robust and efficient. Moreover, although some of the elements embedded in these issues are quantifiable, others can be classified as intangible. Consequently, appropriate techniques are also needed to deal with the information, which is often fraught with uncertainty and subjectivity.
Detailed information can be found on the group's website.
The design of construction components, improved by adding UP waste
The residues from useless pneumatics (UP), overall rubber and textile fibres, contain a great potential for the building sector, due to their thermic and acoustic isolation capacity to a relatively affordable cost.
In this context, the crew of the UPV Multidisciplinary Mathematic University Institute co-directed by Professor Julia Real, works on the development of new indoor insulation elements, along with windows and roof tiles that also contain these materials.
In the first case, researchers work with a tri-layer composition based on recycled rubber and textile fibres, producing materials that provide edification with a remarkable thermic and acoustic insulation. Together with these components, the final product includes additives, producing the mandatory fire resistance legally required.
In terms of windows, they constitute an important element in order to guarantee an adequate thermic and acoustic isolation in a building. Especially, the frame of a window is one of the most delicate elements in this sense. Researchers of IMM develop new frames, based on recycled rubber, which offers excellent results on both sound attenuation and thermal insulation. As in the case of the windows, this product implements particular additives to provide it with a mechanical behavior according to the demands it will have to cover.
Eventually, the roof tiles, based on UN are an excellent alternative to today's market options because its lightness, excellent thermal and acoustic behavior and its low price (due to its ease of fabrication and the low price input). Again, UPV researchers include in these products additives to provide them with different properties, such as immutability before atmospheric elements.
The crew of the UPV Multidisciplinary Mathematic University Institute has a vast experience in the development of research projects and the industrial sector, focused on different UP uses.







